Examples of using catLGM
These demos illustrate the use of catLGM.m function to solve variety of machine learning problems. The code used to generate these demos can be downloaded here.
To run these demos, change directory to catLGM/ and do addpath(genpath(pwd)).
Return to catLGM main pageContents
Binary Classification with Bayesian Logistic Regression
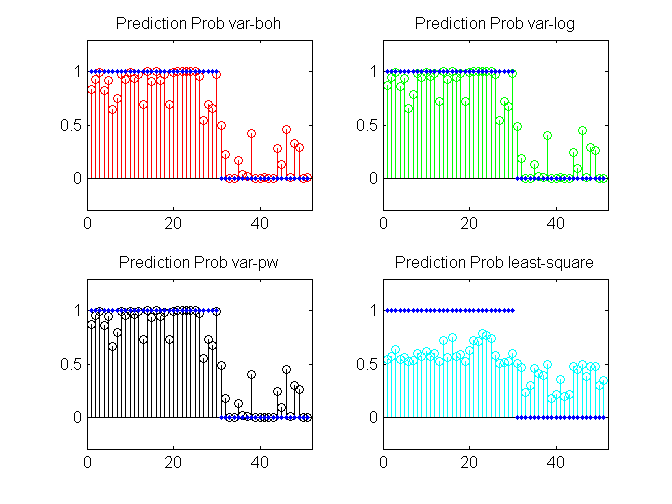
clear all; setSeed(1) % generate data N = 5000; Ntrain = 4000; X = 2*rand(N, 2)-1; y = (sigmoid(X*[1; -1]))>0.5; y = ~y + 1; % Always specify binary data in [1 2] coding instead of [1 0] idx = randperm(N); ytrain = y(idx(1:Ntrain)); Xtrain = X(idx(1:Ntrain),:); ytest = y(idx(4950:end)); Xtest = X(idx(4950:end),:); ytest_bit = bsxfun(@eq, ytest, [1 2]); % specify model, algorithm and options model = 'bayesLogitReg'; algos = {'var-boh','var-log','var-pw'}; options = struct( 'maxItersInfer', 100, 'lowerBoundTolInfer', 0.001, 'displayInfer', 0); % Run each algorithm for i = 1:length(algos) % inference and prediction postDist{i} = catLGM('bayesLogitReg', 'infer', algos{i}, [Xtrain ytrain], options); pred(:,:,i) = catLGM('bayesLogitReg', 'predict', 'mc', Xtest, [], postDist{i}); % compute cross entropy error and store predErr(i) = -sum(sum(ytest_bit.*log2(pred(:,:,i)),2),1)/length(ytest); predProb(:,i) = pred(:,1,i); logLik(i) = postDist{i}.logLik; w(:,i) = postDist{i}.mean; end % least squares with (1,-1) encoding yc = -(2*ytrain-3); % change to (1,-1) w_ls = inv(Xtrain'*Xtrain)*Xtrain'*yc; w(:,end+1) = w_ls; p_ls = sigmoid(Xtest*w_ls); p_ls = [p_ls 1-p_ls]; predErr(end+1) =-sum(sum(ytest_bit.*log2(p_ls),2),1)/length(ytest); predProb(:,end+1) = p_ls(:,1); algos{end+1} = 'least-square'; logLik(end+1) = NaN; % display algos fprintf('Estimated Weights: \n '); w fprintf('Prediction error\n '); predErr fprintf('Training log-lik\n '); logLik % plot [tt1,idx] = sort(ytest); figure(1); clf; colors = {'r','g','k','c'}; for i = 1:length(algos) subplot(2,2,i); stem(predProb(idx,i),'r', 'color', colors{i}); hold on; plot(ytest_bit(idx,1),'.','linewidth',4); xlim([0 length(ytest)+1]); ylim([-0.3 1.3]); title(sprintf('Prediction Prob %s', algos{i})); end
algos =
'var-boh' 'var-log' 'var-pw' 'least-square'
Estimated Weights:
w =
9.4560 11.0330 11.2652 1.0153
-9.4208 -11.0141 -11.2466 -0.9932
Prediction error
predErr =
0.2089 0.1847 0.1812 0.7174
Training log-lik
logLik =
-420.2152 -416.5018 -450.3729 NaN
Multi-Class classification using Bayesian Multinomial-Logit Regression
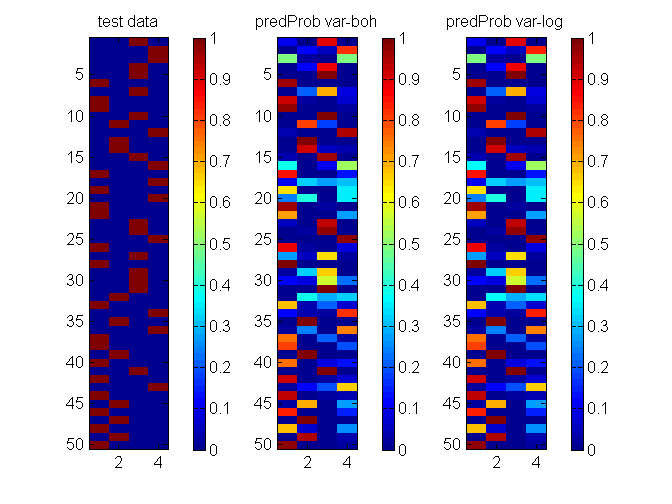
clear all; % generate data N = 1000; F = 5; nClass = 4; X = 2*rand(N, F)-1; beta = randn(nClass,F); eta = X*beta'; lse = logsumexp(eta,2); prob = bsxfun(@minus, eta, lse); prob = exp(prob); [junk,y] = max(prob,[],2); Ntest = 50; Ntrain = ceil(0.8*N); idx = randperm(N); ytrain = y(idx(1:Ntrain)); Xtrain = X(idx(1:Ntrain),:); ytest = y(idx(N-Ntest+1:end)); Xtest = X(idx(N-Ntest+1:end),:); ytest_bit = bsxfun(@eq, ytest, [1:nClass]); % specify model, algorithm and options model = 'bayesMultiLogitReg'; algos = {'var-boh','var-log'}; options = struct('maxItersInfer', 1000, 'lowerBoundTolInfer', 1e-5, 'displayInfer', 0); % Run each algorithm for i = 1:length(algos) postDist{i} = catLGM(model, 'infer', algos{i}, [Xtrain ytrain], options); predProb(:,:,i) = catLGM(model, 'predict', 'mc', Xtest, [], postDist{i}); % compute cross entropy error and store predErr(i) = -sum(sum(ytest_bit.*log2(predProb(:,:,i)),2),1)/length(ytest); logLik(i) = postDist{i}.logLik; w(:,i) = postDist{i}.mean; end % display algos w predErr logLik % plot figure(1); clf; nr = 1; nc = size(predProb,3) + 1; subplot(nr,nc,1); imagesc(ytest_bit); colorbar; caxis([0 1]); title('test data'); for i = 1:size(predProb,3) subplot(nr,nc,i+1); imagesc(predProb(:,:,i)); colorbar; caxis([0 1]); title(sprintf('predProb %s', algos{i})); end
algos =
'var-boh' 'var-log'
w =
5.2856 5.2865
-0.5911 -0.5971
-3.0405 -3.0356
-1.1945 -1.1917
0.5754 0.5728
-4.4748 -4.5063
-4.0890 -4.1053
-2.2287 -2.2379
1.0797 1.0892
-0.9744 -0.9858
3.9102 3.9116
-7.2525 -7.2706
0.3131 0.3162
-3.6087 -3.6150
2.1769 2.1784
predErr =
0.3414 0.3413
logLik =
-303.3138 -301.7505
Multi-Class Gaussian Process Classification
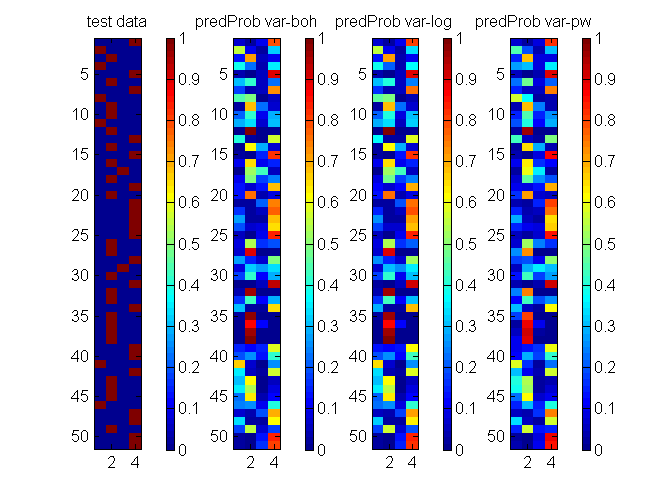
clear all; % generate data N = 1000; F = 2; nClass = 4; X = randn(N, F); beta = [0 0; 1 0; 0 1; -1 1]; eta = X*beta'; lse = logsumexp(eta,2); prob = bsxfun(@minus, eta, lse); prob = exp(prob); [junk,y] = max(prob,[],2); Ntrain = ceil(N*0.1); idx = randperm(N); ytrain = y(idx(1:Ntrain)); Xtrain = X(idx(1:Ntrain),:); ytest = y(idx(950:end)); Xtest = X(idx(950:end),:); ytest_bit = bsxfun(@eq, ytest, [1:nClass]); % mean and covariance functions and their hyper-parameters params.meanfunc = {@meanZero}; params.covfunc = {@covSEiso}; params.hyp.mean = []; params.hyp.cov = 1*ones(nClass-1,2); params.others.nClass = nClass; % Specify model and algorithm models = {'multiLogitGP', 'multiLogitGP', 'stickLogitGP'}; algos = {'var-boh', 'var-log', 'var-pw'}; options = struct('maxItersInfer', 1000, 'lowerBoundTolInfer', 1e-5, 'displayInfer', 0); % Run each algorithm for i = 1:length(algos) inferOut{i} = catLGM(models{i}, 'infer', algos{i}, [Xtrain ytrain], options, params); predProb(:,:,i) = catLGM(models{i}, 'predict', 'mc', Xtest, [], inferOut{i}); predErr(i) = computeCrossEntropy(predProb(:,:,i)', ytest, nClass); logLik(i) = inferOut{i}.logLik; end % display algos predErr logLik % plot figure(2); clf; nr = 1; nc = size(predProb,3) + 1; subplot(nr,nc,1); imagesc(ytest_bit); colorbar; caxis([0 1]); title('test data'); for i = 1:size(predProb,3) subplot(nr,nc,i+1); imagesc(predProb(:,:,i)); colorbar; caxis([0 1]); title(sprintf('predProb %s', algos{i})); end
algos =
'var-boh' 'var-log' 'var-pw'
predErr =
0.6974 0.6864 0.7562
logLik =
-82.1167 -75.2715 -75.8875
Binary Latent Gaussian Graphical Model
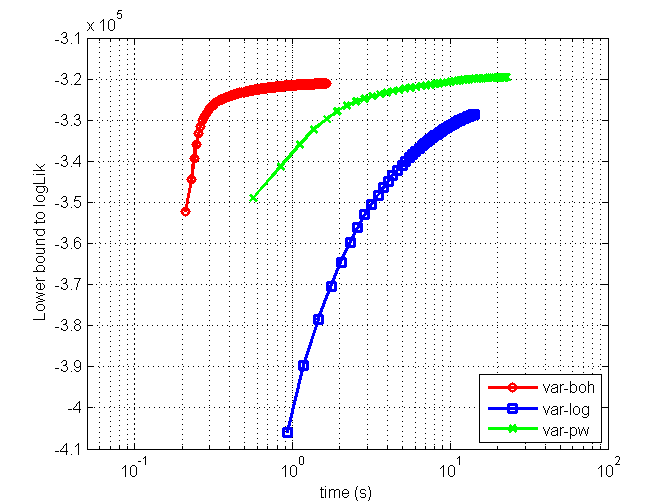
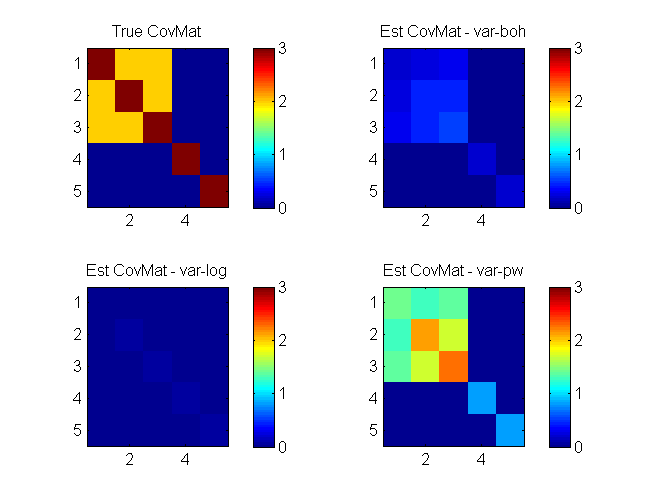
clear all; % generate data D=5; mean_ = [2 1 0.5 0 0]'; X1 = [1 1 1; 0 0 0]; X2 = [0 0; 0 1; 1 0; 1 1]; X=[X1(repmat(1:2,4,1),:), repmat(X2,[2,1])]; C=7*cov(X)+eye(D); covMat = C; S = 100000; z = mvnrnd(mean_,C,S); az = sigmoid(z')'; Y = (az>rand(S,D))'; % Always change binary data to [1 2] coding instead of [1 0] Y = ~Y + 1; % specify model, algos and options model = 'binaryLogitLGGM'; algos = {'var-boh','var-log','var-pw'}; options = struct('lowerBoundTolLearn', 0.01,'displayLearn',0); nIters = [200 50 50]; % run each algorithm for i = 1:length(algos) options.maxItersLearn = nIters(i); out{i} = catLGM(model, 'learn', algos{i}, Y, options); mean_(:,i+1) = out{i}.params.mean; covMat(:,:,i+1) = out{i}.params.covMat; end % plot figure(1); clf; h(1) = semilogx(out{1}.time, out{1}.logLik, 'ro-', 'linewidth',2); hold on h(2) = semilogx(out{2}.time, out{2}.logLik, 'bs-', 'linewidth',2); h(3) = semilogx(out{3}.time, out{3}.logLik, 'gx-', 'linewidth',2); xlim([0.05 100]); grid on; legend(h, algos, 'location', 'southeast'); xlabel('time (s)'); ylabel('Lower bound to logLik'); fprintf('Estimated mean\n'); ['truth' algos] mean_ figure(2); clf; nr = 2; nc = 2; for i = 1:size(mean_,2) subplot(nr,nc,i) imagesc(covMat(:,:,i)); colorbar; caxis([0 max(C(:))]); if i ~=1; title(sprintf('Est CovMat - %s', algos{i-1})); else title('True CovMat'); end end
Estimated mean
ans =
'truth' 'var-boh' 'var-log' 'var-pw'
mean_ =
2.0000 1.3461 0.9507 1.6454
1.0000 0.6766 0.5080 0.9178
0.5000 0.3350 0.2318 0.4774
0 0.0015 -0.0982 -0.0005
0 0.0052 -0.0949 0.0035
Categorical Factor Analysis
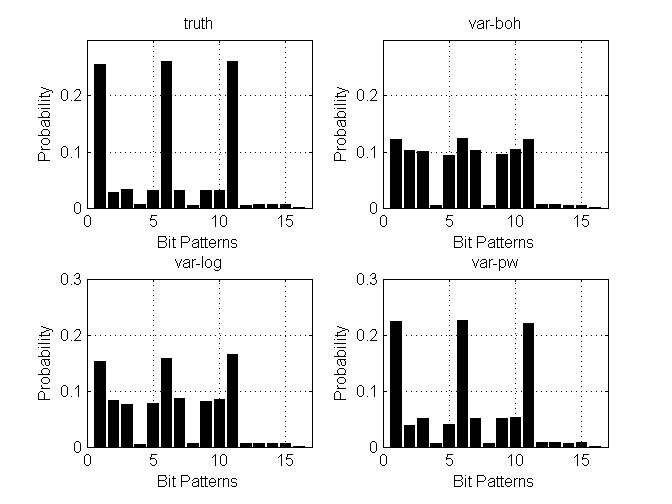
clear all % D dimensions with M categories and N data points D = 2; M = 4; nC = M*ones(D,1); N = 10000; L = (M-1)*D; X = [eye(M-1) eye(M-1)]; C = 20*cov(X) + eye(D*(M-1)); covMat = C; mean_ = zeros(L,1); z = mvnrnd(mean_(:)', covMat, N); for d = 1:D idx = [1:M-1] + (d-1)*(M-1); eta_d = [z(:,idx)'; zeros(1,N)]; lse = logsumexp(eta_d,1); prob = exp(bsxfun(@minus, eta_d, lse)); [junk, Y(:,d)] = max(prob); end Y = Y'; % compute true data distribution [Yt,I,J] = unique(Y','rows'); dist(1,:) = hist(J,1:size(Yt,1))/size(Y,2); % specify models, and corresponding algos and options models = {'multiLogitFA','multiLogitFA','stickLogitFA'}; algos = {'var-boh','var-log','var-pw'}; options = struct('lowerBoundTolLearn', 0.01,... 'displayLearn',0,... 'maxItersInfer',10,... 'maxItersLearn', 100,... 'latentDim', 2); % run algorithms for i = 1:length(algos) out{i} = catLGM(models{i}, 'learn', algos{i}, Y, options); mean_ = out{i}.params.mean; covMat = out{i}.params.covMat; W = out{i}.params.loadingMat; bias = out{i}.params.bias; [dist(i+1,:), Y1] = computeCatDist_mc(models{i}, mean_, covMat, W, bias, nC); end % plot figure(1); nr = 2; nc = 2; subplot(nr,nc,1) bh = bar(dist(1,:), 'facecolor', 'k', 'edgecolor', 'k'); ylim([0 .30]); xlim([0 17]); grid on; hx = xlabel('Bit Patterns'); hy = ylabel('Probability'); ht = title('truth'); for i = 2:length(algos)+1 subplot(nr,nc,i) bh = bar(dist(i,:), 'facecolor', 'k', 'edgecolor', 'k'); ylim([0 .3]); xlim([0 17]); grid on; hx = xlabel('Bit Patterns'); hy = ylabel('Probability'); ht = title(algos{i-1}); end
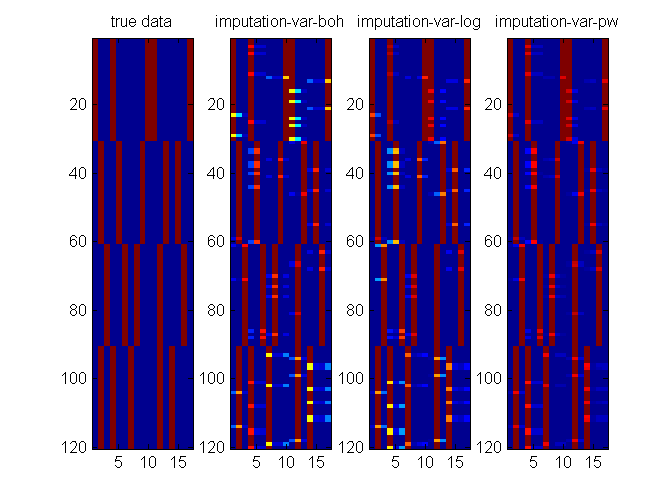
Missing data imputation
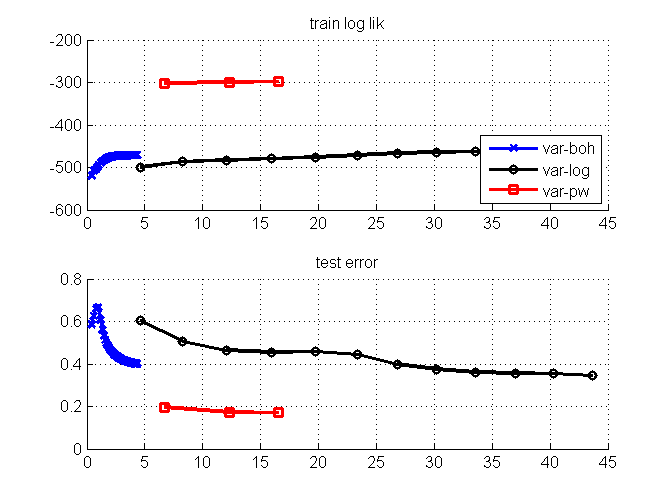
clear all; close all; % genearate data Y = [ repmat([1; 1; 4; 1; 4], 1, 30)... repmat([2; 2; 3; 3; 2], 1, 30)... repmat([3; 3; 2; 2; 3], 1, 30)... repmat([2; 1; 1; 2; 1], 1, 30)]; nC = [3; 3; 4; 3; 4]; Ybitvec = encodeDataOneOfM(Y, nC, 'M'); [D,N] = size(Y); % create one missing entry in part of the data d = unidrnd(D,1,N); % one missing dim in each data point ratio = 0.5; % ratio of missing data examples Ymiss = Y; nMiss = 0; for i = 1:size(Y,2) if rand <ratio Ymiss(d(:,i),i) = NaN; nMiss = nMiss + length(unique(d(:,i))); % #miss end end % specify models, algorithms, and options for imputation models = {'multiLogitFA', 'multiLogitFA', 'stickLogitFA'}; algos = {'var-boh', 'var-log', 'var-pw'}; colors = {'bx-','ko-','rs-'}; nIters = [35 12 3]; options = struct('maxItersLearn', 5,... 'lowerBoundTolLearn', 0.001,... 'displayLearn',0,... 'maxItersInfer',10,... 'maxItersMstep',5,... 'latentDim',5); % plot true data figure(2); clf; nr = 1; nc = length(algos)+1; subplot(nr,nc,1); imagesc(Ybitvec'); title('true data'); figure(1); clf; % data imputation for m = 1:length(algos) fprintf('EM for Parameter learning\n'); params = []; initVec = []; algos{m} for iter = 1:nIters(m) % warm start from previous iterations of EM options.initVec = initVec; % learn model learnOut = catLGM(models{m}, 'learn', algos{m}, Ymiss, options, params); % read output params = learnOut.params; % learned parameter postDist = learnOut.postDist; % post Dist initVec = learnOut.ss.initVec; % for next iteration trLogLik(iter) = learnOut.logLik(end); tt(iter) = learnOut.time(end); % impute data pred = catLGM(models{m}, 'impute', 'mc', Ymiss, [], params, postDist); err(iter) = -sum(sum(Ybitvec.*log2(max(pred,eps))))/nMiss; % plot figure(1); subplot(2,1,1); hold on h1(m) = semilogx(cumsum(tt), trLogLik, colors{m}, 'linewidth',2); grid on; title('train log lik'); subplot(2,1,2); hold on grid on; semilogx(cumsum(tt), err, colors{m}, 'linewidth',2); title('test error'); drawnow; figure(2); subplot(nr,nc,m+1); imagesc(pred'); title(sprintf('imputation-%s', algos{m})); drawnow; end clear err trLogLik tt; end figure(1); subplot(2,1,1); legend(h1, algos, 'location', 'southeast');
EM for Parameter learning ans = var-boh EM for Parameter learning ans = var-log EM for Parameter learning ans = var-pw